画像の演算と離散化誤差
ベクトルデータの「線」は、直交座標上で始点と終点を結ぶものとして定義され、物理的な大きさに対応する画素とは無関係な理念上の線なので、水平・垂直の線と斜めの線は質的に全く等価となります。しかしビットマップ（ラスタ）データでは、有限個数で実体として面積を有する画素（ピクセル）に依存するため、水平・垂直の線と斜めの線では質が異なります。例えば、水平・垂直は、ピクセルの配列方向と一致するので綺麗に表示されます。一方、斜めの線は有限な大きさを持つ矩形のピクセルに制約されて、ギザギザが出てしまいます。 このギザギザが、本来の正当なデータなのか或いはピクセルの制約から来るノイズで本来は綺麗で滑らかな線なのか、データ処理システムには判断できません。このため、ラスタデータをベクトルデータに変換しようとするとき判断に困ると言う深刻な問題が生じます。
AD変換では、連続アナログデータを離散デジタルデータに変換しており、「サンプリングレート」はピクセルのサイズ設定、「量子化レベル」の設定はカラー深度に関係し、変換に際して連続データの一部が廃棄される「不可逆圧縮」となります。このため、一旦離散化されたデータからは、完全に元のデータに復旧できないという制約があり、「サンプリングレート」と「量子化レベル」の設定には綿密な注意が必要です。
RGBからYUVへの返還も同様で、値域が同じでも定義域が異なるためYUVからRGBへの逆変換では元のデータに戻ることはほとんどないという現実があります。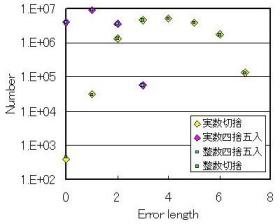右図にRGBからYUVに変換してさらに逆変換を行った際、元の輝度とどの程度ずれるのかについて計算した例を示します。画素が縦横上下方向に一つずれたら１、斜めにずれた場合には２として計算した結果です。係数は倍精度の実数で計算し、小数点以下を切り捨てて計算した場合には、完全に元に戻るデータはわずか395個、0.5で四捨五入した場合には４万個弱と全体の24％弱が元に戻るのみです。
四捨五入で演算した場合には４画素以上ずれる例は存在しなかったので、計算精度的には十分な精度と考えられますが、変換マトリックスを倍精度で計算してこの程度の誤差になるということに留意しておく必要があります。小数点以下を切り捨てる場合にはさすがに誤差は大きくなりますが、この場合には８画素以上ずれるものは存在しませんでした。マトリックスの係数を1000倍して整数計算を実施した結果も実数計算をした結果も整数演算の方が誤差は若干大きいもののほとんど差異は存在しません。ただし計算結果が、[0-255]からはみ出る場合も必ず存在しますから、正確に計算するためには例外処理が必要となります。
次ページ 2014.10.10作成 2017.1.25改定