6.1 整数演算誤差
ＲＧＢからＹＵＶへの変換を整数で行う場合の注意点について説明します。普通の画像データは８ビット（１バイト）の正の整数で扱われます。演算も正の整数で実施する方が計算時間が速くなるのと実数と整数との変換をせずに済むのという利点があります。ただし、正の整数と符号付きの整数を時々間違えて思わぬ計算エラーが出ることがあるので、この点に注意が必要です。ＹＵＶの値を1000倍の整数で取り扱うときの演算式は以下のようになります。私自身はＵＶについては下記の演算で得られた値を１０００で割り戻して１バイトの正のキャラクターとして取り扱っています。Ｙに関しては、次節でも平坦化やエッジ強調など各種の演算を実施する必要があり、下記の演算を１０で割り戻して２バイトの正の整数として取り扱っています。その根拠を以下で説明します。
Y = 299*R + 587*G + 114*B
U = -169*R - 331*G + 500*B + 128000
V = 500*R - 419*G - 81*B + 128000
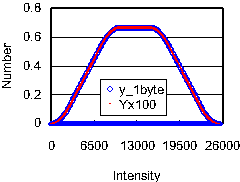
右図にＲＧＢ色立方体をＹＵＶ変換したＹ値のヒストグラムを示します。ＲＧＢ各色の平均は128なので、ＲＧＢのヒストグラムをこの図に表示すると0.39の直線上に表示されることになります。ＹＵＶ変換した後の輝度の分布は、０及び255（図の数値では25500）で低く中央部で高い分布となります。１バイトで取り扱った時の分布と２バイトで取り扱った時の分布はほぼ一致しています。２バイトの場合には輝度の両端付近で対応しない輝度が発生します。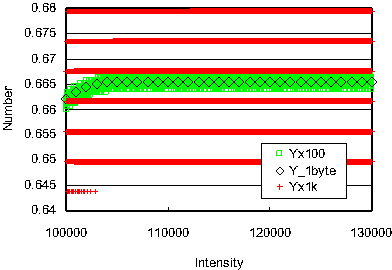
1000倍の取り扱いでは輝度が存在する個数は247,024個（欠損数は7,977個）、100倍（＝２バイト）では25,316個（欠損数は185個）、10倍では2,550個（欠損数は1個）となります。右図は輝度が100から130の範囲を拡大して表示した例を示します。この場合には1000倍した時には整数誤差で輝度分布が若干ばらつくのに対して、２バイトに割り戻した場合にはばらつきがかなり抑制されることが分かります。最終的には１バイトのデータに変換するため、データのばらつきに対しては裕度は高くなりますが、データの取り扱いの優位性と誤差が顕著に少なくなることの両面から、Ｙについての計算途中でのデータ精度は２バイトを採用することが好ましいと考えています。
画像を取り扱うためには、色の変換だけではなく、画像内部の座標系の変換も必要になります。３次元形状モデルをディスプレイや印刷面などの２次元平面に投影する投影変換（projective transformation）はモデリングされた形状をディスプレイ表示あるいはプリンタ印刷の際に良く用いられます。３次元形状モデルが定義された局所座標系を、平行移動、回転移動、拡大・縮小変形などを行う変換が幾何変換（geometric transformation）で、異なる座標系でモデリングされたパーツを全体座標系で組合せるか分解する際に用いられます。視点の位置あるいは投影する方向（視線の方向）を移動・回転する変換が視野変換(viewing transformation)です。
ｎ次元空間上の点 P (x1, x2,…, xn) に対して新たな量Ｗを導入し以下の関係に基づいてｎ＋１次元の直交座標系で各点 (X1, X2,…, Xn , W) を表現する方法を同次座標（homogeneous coordinate）表現と言います。わざわざ次元を増やすのは無駄に感じられるかもしれません。大雑把な説明をすると、平面にはいつくばった状態では平面の広さを実感できませんが、平面の外に出て平面を俯瞰的に眺めると、その平面を理解しやすくなります。このような感覚で同次座標系を考えればよいのではと思います。
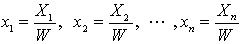
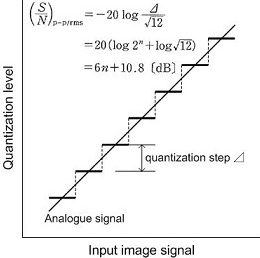
付け足しになりますが、Ａ／Ｄ変換では、連続量である電圧信号を離散的なデジタル数値に変換します。このため、離散化誤差は避けることができません。変化率の大きい画像データに対してはビット数の小さい離散化でも見た目に大きな影響はありません。一方、微妙な変化しかしていないデータを離散化する場合には、変化量に対応した精緻なビット数で変換しなければ意味のある変換にはなりえません。
換言すると、大雑把な変化を把握することが必要なときには細かいことには目をつむり、あまり変化が無いように見える局面では些細なところに注意が必要「悪魔は細部に潜む」と言うことです。パッと見たときの印象が以外に正確な判断となります。
次ページ 2014.10.10作成 2018.9.9改定