6.4 投影変換
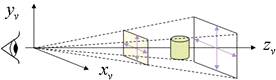投影変換には、視点を zv 軸上に置き、zv 軸に垂直な面に投影する透視投影変換(右図)と視点を全体座標系の z 軸上無限遠方に置き、 zv 軸に垂直な面に投影する平行投影変換の２種類あります。
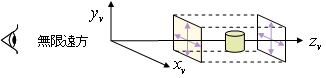
右図は無限距離の視点からの平行投影変換です。
投影変換に必要な座標系として、３次元モデルを定義する座標系（右手系）＝全体座標系（world coordinate system）: (x, y, z)と、視線を zv 軸とした座標系（通常，左手系）＝視座標系（viewing coordinate system）: (xv, yv, zv)、さらに隠面・隠線処理で必要となる視座標系の可視領域を正規化した座標系（通常，左手系）＝正規化視座標系（normalized viewing coordinate system）: (xnv, ynv, znv)があります。
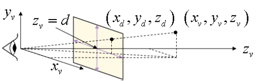
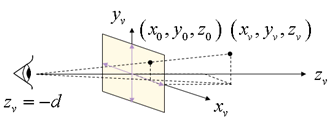
透視投影変換では、視点と投影面の位置を違えた２つの変換が使われており、通常使われるのは視点を原点に置き（ze =0）、投影面を原点からｄの距離（zv =d）におく変換です。右上図は通常の透視投影変換（視点が原点）です。
視点が原点（ze=0）のとき、対象物の座標 (xv, yv, zv) と投影点 (xd, yd, zd) の関係は次式となります。
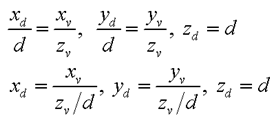
これらの関係は同次座標を用いて次式で表せます。
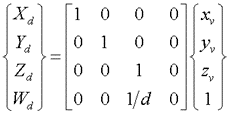
投影面を原点（zv=0）とし視点を原点からｄの距離（zv=-d）に置く変換では、対象物の座標(xv, yv, zv) と投影点 (x0,y0,z0) との関係は次式のようになります。この場合、視点が無限遠の時に平行投影変換となります。
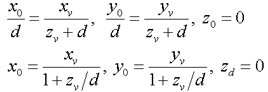
これらの関係は同次座標を用いて次式で表せます。
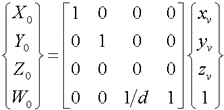
以上説明してきた各種の変換を(4x4)行列を用いて演算することにより必要な情報に変換されます。
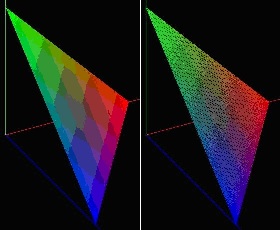これらの変換を実行するときに留意しなければならないことは、最終的な値域をきちんと判別して、その値域内の各画素が元々のどの画素に対応しているのかを見極めて変換を行うことです。通常は元の画素とぴったり一致することはまずありませんから、(x, y)座標の小数点以下の数値を用いて比例配分して色を対応する操作が必要となります。もともとの対象物の定義域の座標の値を機械的に変換してしまうと、右図の右半分の画像のように最終的な画像の中にデータ欠損部（色平面上のぶつぶつの黒い点）が多数含まれることになります。
次ページ 2014.10.10作成 2017.6.27改定