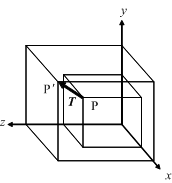同次座標を導入する理由は、平行移動、回転移動、投影変換などの変換を、行列を用いて表現できるためです。
点Ｐ(x,y,z) をＴ＝（Tx,Ty,Tz）だけ平行移動した点Ｐ’（x’,y’,z’）は同次座標表現を用いて次式となり、線形行列で表現できますので、計算の見通しが良くなります。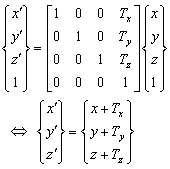
回転移動については以下のようになります。
点Ｐ（x,y,z) をｘ軸，ｙ軸，ｚ軸の方向に向いて、時計方向（右回り）に θx,θy,θz回転した点Ｐ’ (x’,y’,z’)は、
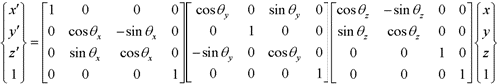
のように表現できます。一つ一つの回転ごとに式を記述できることにより、全体の見通しがすっきりします。
ｘ軸,ｙ軸,ｚ軸に対して Sx,Sy,Sz 倍する拡大・縮小の場合には、次式で表現できます。
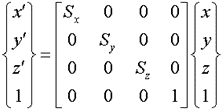
x 軸場合に対して反転した場合
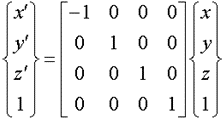
原点に対して反転した場合には
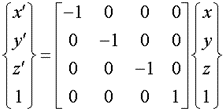
となります。
次ページ 2014.10.10作成 2026.01.18改定
・アフィン変換(affine transformation)は線型変換(回転、拡大縮小、剪断)と平行移動の組合せです。
・アフィン(affine)はラテン語で「類似・関連」を意味する affinis に由来します。
・「線型変換」は線型写像とまったく同義と扱われる場合もあります。始域と終域を同じくする線型写像の意味で用いることもよくあります。
・立体視の仕組みはホイートストンによって1883年に解明されました。人間以外の動物も立体視を用いていることが明らかになったのは、1970年になってからでした。
・1983年にはウスバカマキリに専用の３Ｄ（左右緑と青の組合せ）メガネを装着して１点づつの緑と青の点をＰＣ画面上で操作し、点が画面から飛び出して見える錯覚を利用して、ウスバカマキリが立体視を行っていることを解明しました。アリの放浪記（オドレー.デュストゥール他；山と溪谷社）には、人間の無意識の優越性に起因する思い込みを修正する記事がふんだんにあり、息抜きに読むことをお勧めします。