６．画像の演算と離散化誤差　　　　　6.3　回転移動

前ページ

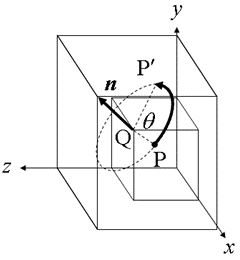　任意の軸回りの回転移動について整理します。右図に示した点Ｐ(x,y,z) を点Ｑ(xQ,yQ,zQ) を始点とする単位ベクトル ｎ＝(nx,ny,nz) に対して時計方向に θだけ回転した点Ｐ’ (x’,y’,z’) への変換の場合には、以下の手順に分解して整理できます。
手順１：点Q (xQ,yQ,zQ) を原点に平行移動する

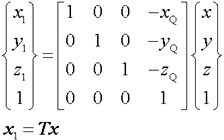
手順２：単位ベクトルｎ＝(nx,ny,nz) をｚ軸回りに α だけ回転してｙ−ｚ平面内に移動する（n1ベクトルとする）

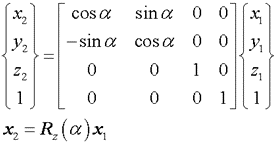
手順3： n1ベクトルを x軸回りに βだけ回転して x軸と一致させる（n2ベクトルとする）

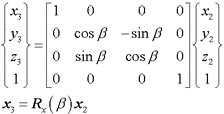
手順4： n2ベクトルを z軸回りに θ だけ回転する

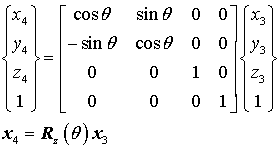
　回転や拡大縮小あるいは平行移動などを要素ごとに分解して行列を作成して順次掛け合わせることで最終的な変換が次式のように完成します。このように線形変換の組合せで表現できることで見通しがすっきりします。

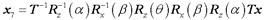
次ページ　　　2014.10.10作成　2017.6.27改定