９．２ 液滴領域の抽出
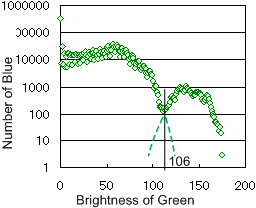前節で、現在対象として考えているビデオデータの場合には、緑色座標と青色座標の値を比較することにより液滴領域を抽出できる可能性を指摘しました。右図に液滴が存在する高さの領域に存在する各画素の緑色の値の輝度分布を示します。輝度値１０６の線より左側が液滴以外と考えられる輝度分布で右が液滴の輝度と推定しました。それぞれの輝度分布に緑色の破線で外挿した線分で表示した領域が液滴が存在しない領域及び液滴領域の本来の輝度分布と考えられます。
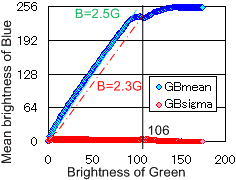
右図は各画素の緑色の値に対して青色の輝度値がいくらであるのかについて検討して、それぞれ平均値と分散とを計算して、右図に表示しました。この図から明らかなように青色の輝度値が飽和していない場合には、青色の値は緑色の約２．５倍になっています。液滴の挙動をカラー撮影する場合には、アークなどから液滴部分を明瞭に撮影するために色々な撮影条件を試した結果、露出オーバーの撮影条件が選ばれることが良くあります。輝度値を定量的に解析する場合には露出不足気味に撮影条件を選定することを推奨しています。しかし、液滴移行形態の解析ではこの撮影のように露出オーバーにした方が映像特に見たい領域が鮮明に撮影されるために、挙動説明に説得力があります。
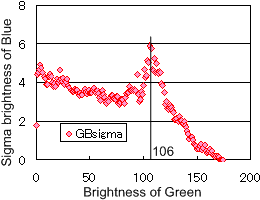
青色のばらつき具合の指標である分散を同じ図に赤で示しています。その値が平均値に対して極めて低く、液滴とそれ以外の領域とを区分けする指標として好ましい条件であることを示唆しています。平均値に対する分散の値が極めて低く、傾向が判別しにくいため、右図に分散のみの図を示します。
平均値と分散値を比較検討した結果、各画素における緑色の輝度値が１０６以下で、青色の値が緑色の２．３倍より高い画素はアーク領域であり、２．３倍より低い画素が液滴である可能性が高いと判断できます。また、緑色の値が１０６以上は全て液滴と判断して良さそうです。しかし、これらの条件だけではワイヤから液滴が離脱する時点で液滴周囲に存在する液滴の輝度に近いアークとの分離がうまくいかない可能性が存在します。以下では、液滴と液滴周囲のアーク領域の分離法について検討します。
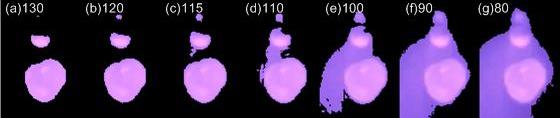
下に示す画像は、左から緑色の輝度値がそれぞれ(130,120,115,110,90,80)より低い画素の各色(R,G,B)の値を０にして、液滴離脱直後の状況を離脱領域近傍についてのみ表示した例です。閾値を１２０以上にした場合には、液滴（溶融金属）領域が完全に分離できており、１１５ではアーク領域の一部が残り、１１０以下の閾値ではアーク領域がかなり残存していることが分かります。
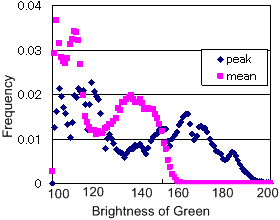右図は、上図の（ｅ）に示してある閾値１００を基準として、各瞬間の映像の全画面について水平方向に走査して閾値１００以上の画素をピックアップし、各水平線上のデータの最大値と平均値を集計した結果です。各水平軸上でのピーク（最大）値はかなりばらついています。平均値を見ると輝度１２０あたりのところに極値が存在しています。上図（ｂ）でも液滴領域が完全に分離できており、この値（１２０）を閾値にすることが妥当なように感じられます。
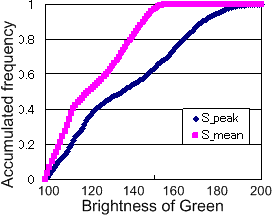
右図は上のデータを累積度数として表示した例であり、ピーク値の累積度数分布が輝度１２０近傍で変極点があるように見られることからも、この値が妥当であることを裏付けています。平均値の累積度数データでは変極点は１１５近傍に存在し、累積度数が同じところで変極点が存在していることもこの類推の妥当性を示しているように思えます。
液滴領域特定のための閾値をいくらにすることが物理的に妥当なのかは常に議論になり、その一つの方法として以下のようなものがあります。
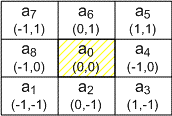
右に示すような（３×３）の画素領域について、中心の点a0の輝度値とその領域内の画素９個の最大値と最小値との差をプロットして、差が最大となる輝度値を閾値とする方法です。右下の図に結果の一例を示します。ここで注意しておかなければならないのは、機械的に計算を実施すると、領域の境界近傍での差を抽出したいのに、実際の計算結果には領域内部での差の影響が強く出る点です。
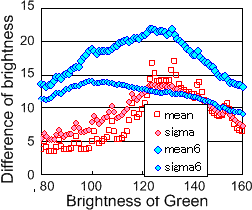
右図の赤い色で示したマークは機械的に計算した結果の例で、領域周辺では差が大きく、領域内部では差があまり大きくは無いために、機械的に計算した場合には平均値より分散の方が大きくなる結果が得られています。青色でプロットした関係は、機械的な計算結果も踏まえて領域内部での差は境界周辺部より差は小さいと考え、最大値と最小値の差が５より大きい画素のデータのみを計算した結果です。当初期待したほどの大きな差は見られませんが、閾値を１２０から１３０程度にすることがよいだろうとの結論が得られています。これは、上に示した液滴領域を抽出した結果とも符合しています。
次ページ 2017.7.1作成 2017.7.20改定
