4.8 RGB-YUV変換
輝度と色度の扱い方をYUVの後に続く数字で示すことが多く、YUV42(Y=4, U=2, V=2), YUV12（Y=4, U=1, V=1)などのＹＵＶ変換があります。YUV12は、一般的な8bitで量子化した場合に1ピクセルあたり12bitであるため、こう呼ばれます。輝度信号と色信号とに対する人の感度の違いについては次節で詳細を紹介します。
図にYUV表色系の概念図を示します。(R,G,B)[0,255][0,255][0,[255]の座標系から(Y,U,V)[0,255][0,255][0,255]への線形変換なのですが、YUVの取りうる値(値域)に制限があります。図の左にYUV表色系に変換されたRGB色立方体をY軸の上から見た映像、右に下から見た映像を示します。色立方体を縮小回転に近い写像により[0,255]x3空間の中に閉じ込めており、YUV空間の中で利用されない値域が多く存在します。図中では写像されない領域を黒く表示しています。両方の図は色差を表現する座標系ですから、RGBとその補色が等しい角度で並び、６角形を形成していることが分かります。この二つの図を見ただけでは立方体の単純な縮小回転返還と誤解しやすいのですが、
実はそうではなく、複雑な写像となっています。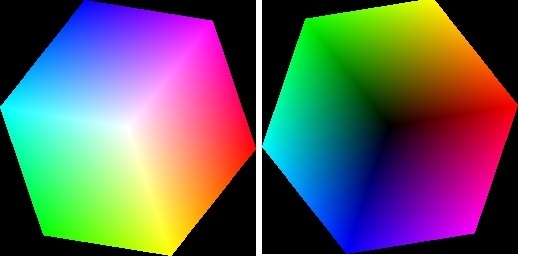
下図に
V軸の両端からYU座標系を眺めた図を示します。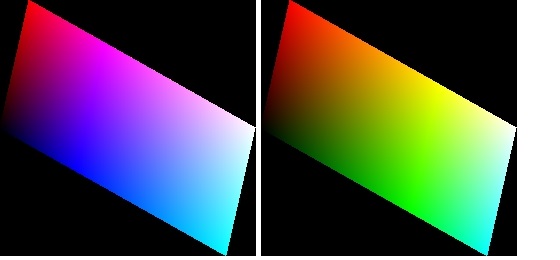
下図には
U軸の両端からYV座標系を眺めた図を示します。
これらの図はすべてY=0を左端、Y=255が右端になるように表示してあります。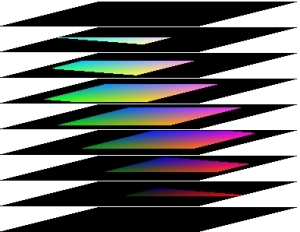
黒地はデータが存在しない領域で、Y=0に近い領域ではデータの有無の判別が難しくなりますが、データが存在する領域は平行四辺形の内部になります。
実際の写像計算においては、整数を取り扱うことによる離散化誤差も含まれるために、RGBからYUVへの変換において1677万7216色から400万7737色へと約24%にデータ数が少なくなります。このうち整数演算による離散化誤差、具体的には図に示されている色空間内部での欠損データ、は64,000個程度となり、YUV色空間内部のデータの約1.6%に相当します。
計算によってある色空間から別の色空間への変換は簡単に実行できますが、変換後の色空間で表現できない色の情報は失われてしまいます。また、その計算は離散的な整数値通常は[0-255]の８ビットの数字を使う関係上、多くのデータ情報の欠損が生じ、不完全なものです。色を扱うにあたっては、なるべく色空間を統一して作業することが大切ですが、RGBとYUVの返還は頻繁に行われますので、その特徴と問題点を認識しておくことが必要です。
色を考える場合に、明るさと独立した色度平面内のRGBを取り扱うこともよくあります。各３原色を３原色の和で除して無次元化すると、除した値r,g,bの和は１となり、２次元平面であらわされます。この平面を色度平面(Chromaticity Plane)と呼びます。
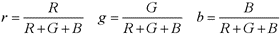
ｒ＋ｇ＋ｂ＝１
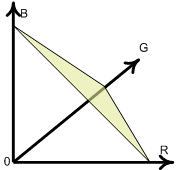
画像内の対象を識別する場合、明るくても暗くても同じ色を判別したい場合には、明るさの情報を除外した四輝度を用いる場合の方が有効なことも多く存在します。右図はＲＧＢ色立方体から色度平面への写像を表現した図で、３原色の純色の頂点(255,0,0), (0,255,0), (0,0,255) を結ぶ平面が色度平面となります。下図は実際にＲＧＢ色立方体の３原色の頂点を結んだ断面を表示した例です。この場合中央の無彩色の点の輝度は(85,85,85)とあまり明るくないので明瞭な白にはなりません。
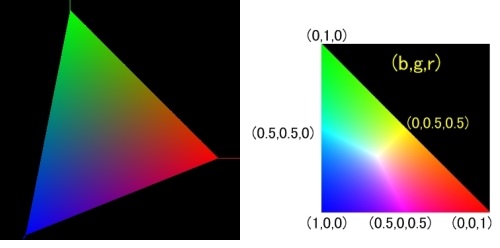
右図は、色度平面上の色をその色度でもっとも明るい色を用いて表示した例です。この３角形の色度平面の中の隣り合う点どうしの関係を保ったままで変形すると、各種の色相関の図形になります。
次ページ 2014.10.10作成 2018.4.11改定