３．４ 粒子の衝突
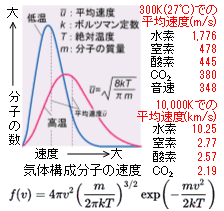気体の個々の粒子の飛行速度は一様ではなく、速いものから遅いものまで様々な速度で飛び回っています。一般的には右図に示すようなマックスウェル・ボルツマンの速度分布則に従います。同種の分子だけで構成される気体では、温度だけで速度分布が決まり、温度が高くなると平均速度は大きくなり、分布範囲は広がります。気体の粒子はあらゆる方向に飛行し、方向性はありません。マックスウェル・ボルツマンの速度分布則を導出することは難しいのですが、図中に示した式で与えられます。気体の二乗平均速度ｕはマックスウェル・ボルツマン速度分布則の平均速度と同じではありませんが、類似の値が求まります。
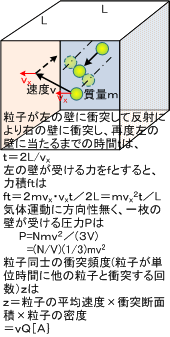
長さＬの立法形の箱の中に質量ｍの粒子が速度ｖで飛行する時、壁には何度も粒子が当たり反発していきます。完全弾性衝突と考えるとＮ個の全粒子により一枚の壁が受ける圧力は右図の式で表されます。この簡単な式を求めるには、数学的物理的な単純化・理想化が行われており、厳密に成立するか否かは本当は面倒くさい話ですが、単純に平均速度を用いることが現実的に物事を考える上では正しいだろうということになっています。
実在の気体では単一元素構成のものはなく、一部はイオン化しており、気体を構成する個々の粒子は複雑な挙動をしています。通常の生活では気にも留めないのですが、地球には遠くの銀河から多くの宇宙線が到来しており、放電開始挙動は宇宙線による電離が引き金になる場合も多くあります。現実の気体は複雑なものですが、全体としてシンプルに考えるのが、工学の立場で物事の本質を理解するための近道で、通常は理想的な気体を想定して考えを進めていきます。その一例が状態方程式です。ボイルの法則は、温度が一定のときには「一定量の気体の圧力Ｐと体積Ｖは反比例する」というものです。シャルルの法則によると、「圧力が一定のとき、一定量の気体体積は絶対温度Ｔに比例」します。両者を合わせたボイル・シャルルの法則では、「一定量の気体体積Ｖは圧力Ｐに反比例し、絶対温度Ｔに比例」します。この関係を理想気体について定量化したものが気体の状態方程式で、ＰＶ＝ｎＲＴという式で表現されます。Ｒは気体定数と呼ばれており、用いる単位系によりその値が異なります。圧力を気圧(atm)、体積をリットル、物質量ｎをモルとするとＲの値は0.082となります。
水を例にして、状態の性質を考えて見ます。水のモル質量は18ｇで１モルの分子数は6.02×10^23個です。液体の場合、１立法センチ(cm^3)で１ｇなので、１立法センチ内には水粒子3.3×10^22個が存在します。水粒子間の平均的な距離は3.11×10^-10mとなります。気体の場合、１気圧・０℃で１モルが占める体積は22.4リットルですから、１立法センチ内には水蒸気粒子1.27×10^19個が存在します。水蒸気粒子間の平均距離は3.34×10^-9mとなります。液体から気体に変態すると、体積で1244倍、分子間距離で10.7倍程度に膨張します。
壁にかかる圧力は単位面積あたりの力ですから、結局圧力Ｐは、気体の体積Ｖ(V=L^3)を用いて、
Ｐ = F/L^2= Nmv^2/(3V)=(N/V)(2/3)(1/2)mv^2
が求まります。
一方、この気体のモル数をｎとすると、理想気体の状態方程式はＰＶ＝ｎＲＴ（ここでＲ は気体定数、Ｔは絶対温度）となります。そしてアボガドロ定数をN_Aとすれば、N = nN_A ですから、これらの式を組合せて
1/2 m v^2 = 3/2 kT ここで k = R/N_A はボルツマン定数。
となります。
以上のような素朴な扱いでボイルの法則のみならず、理想気体の状態方程式と組合せて熱平衡状態での１分子の運動エネルギーの平均のような微視的な量と温度のような巨視的な量とを結びつけることが出来ます。なおこの式は、熱平衡状態では運動の任意の１自由度に kT/2のエネルギーが分配されるという、古典統計力学のエネルギー等分配則の一表現ともなります。
理想気体を考えると、構成粒子の飛行速度の平均値は温度のみで決まり、圧力は仮想的な壁に当たる粒子の個数(密度)と平均運動量の積で決まることになります。気体やプラズマを考える場合には、飛行速度と密度の他に、構成粒子同士がどの程度の頻度で衝突を繰り返すのかを知ることが重要となります。同じ種類の粒子が衝突するのは、相手の直径と自分の直径の和の範囲内を通過する場合となり、この領域の面積を衝突断面積といいます。同じ粒子なので衝突断面積の半径は粒子の直径となります。粒子同士はお互いに飛行していますから、粒子の平均速度は二つの粒子の相対速度の平均値を用います。地上空気の78％を占める窒素分子について考えると、窒素分子の相対速度は670m/s、見かけの直径は0.38nmで衝突断面積Ｓ(=πｒ^2＝3.14x0.38x0.38）は4.5x10^-19m^2になります。理想気体の方程式から窒素の密度は2.4x10^25m^-3と与えられ、１個の窒素分子が単位時間に衝突する頻度ｚは7.2x10^9/sとなります。粒子が衝突してから次の衝突まで飛行する平均距離を平均自由行程λと定義します。この平均自由工程は、平均速度を衝突頻度で割ったもの(λ＝ｖ／ｚ＝670/7.2x10^9=9.3x10^-8m=93nm）です。空気中の窒素は、自分の直径の約245倍飛行すると他の粒子に衝突していることになります。
さて、壁への衝突に戻ります。単位面積の仮想的な壁を考えます。右から左にＮ個の粒子が平均速度ｖで壁に衝突します。実際には粒子は壁で反射されますが、ここでは仮想的な壁なので粒子はすべて通過すると考えます。同時に壁の左側の領域から同様にＮ個の粒子が平均速度ｖでやってきて仮想的な壁を通過します。この状態は実際に壁が存在し、そこで完全弾性衝突により反射されるのと同じことになります。単位体積当たりにＮ個の粒子が存在しているので、壁を１秒間に通過する粒子の個数はＮｖ個となります。この個数は、壁に反射する個数と同じものです。窒素分子は１立方センチ当たり2.7x10^20個存在し、その平均速度は445m/sなので、１秒間に1.2x10^24個の窒素分子が壁に衝突していることになります。このように気体粒子が固体表面に衝突する頻度（確率）は、空間内で粒子同士が衝突する頻度に比べて格段に大きいことに注意が必要です。
次ページ 2016.03.12作成 2017.04.12改訂