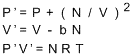４．１ 固体の結合
水中溶接切断をきちんと理解するためには、物事の基礎である物理や化学をきちんと勉強する必要性があることを年をとると共に痛感しています。問題は私の身近にある教科書類の内、基礎系の科学書には、純粋な系、単純な系についての言及しかなかったことです。技術的な観点から本質を理解したいとは思っていましたが、締め切り時間の関係もありどうしても既存の知識範囲のみでの問題解決をせざるを得ませんでした。
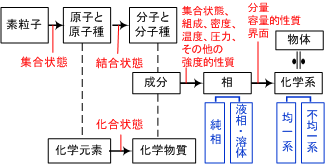
溶接切断はある意味化学的な反応系であり、しかもその反応は非定常なものが多く、反応に関与する素材が非常に多いという、典型的な複雑系の反応です。それらを理解するためには、素粒子レベルの極小サイズから眼に見えるマクロな系さらには強度計算などの構造物全体の大きさあるいは構造物の存在する自然環境の巨大なスケールでの知識も必要となります。実際に個々人が理解でき取り扱える範囲は高が知れていますから、専門的なことはその道の専門家に教えてもらって最善を尽くすしかありません。しかし、大まかな考え方や、その専門家に任せても大丈夫な範囲を理解しておかなければ、まさかの事態を引き起こす危険性が高いことは、昨今の大事故を見れば自明なことです。
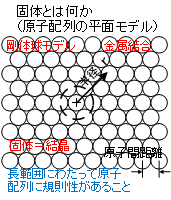
溶接切断の目的は、鋼材の目的に応じた適切な構造に加工することです。溶接の対象である、加工材料は多くの元素を不均一に含有し、その表面にも多量の酸化物が付着しています。その悪条件下で良質な結果を得たいと思っていましたが、なかなかその時に求めていた結論を含んだ書籍を見つけることは困難でした。溶接関係の書籍は単に欠陥を回避するための諸方策が述べられているだけで、物理的な裏づけを理解することはできませんでした。単に私の基礎学力と能力が不足していただけではあります。一番問題であったのは、材料内部の原子レベルでの挙動が全然理解できていなかったことです。水素などの微細な原子が、固体状態の金属組織内で何故動けるのか、凝固時に非金属成分がどのように振舞うのか、てんでんばらばらに凝固していく小さい結晶粒がどのように成長し、その時不純物がどのように振舞うのかについて全然理解できていませんでした。
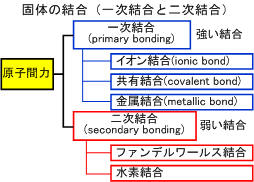
それらの反省を踏まえて、定年後の自由に使える時間を利用して基礎的な事柄の理解に努めてはいますが、ゴールは全然見えてこない状況です。さて、固体の結合では、右図に示すように原則として原子同士に作用する力で原子同士が結合します。
イオン結合と共有結合とについては、以下の説明文と右の結合状態を説明するポンチ絵を見比べれば、何となく分かったような気持ちになれます。
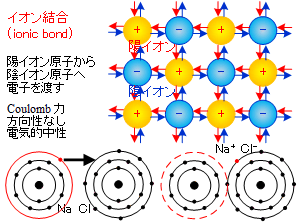
「イオン結合は正電荷を持つ陽イオン（カチオン）と負電荷を持つ陰イオン（アニオン）の間の静電引力による化学結合であり、この結合でイオン結晶が形成される。共有結合と対比され、結合性軌道が電気陰性度の高い方の原子に局在化した極限であると解釈することもできる。」
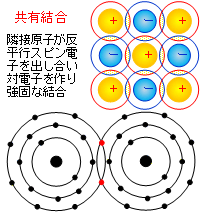
「共有結合は、原子同士で互いの電子を共有することによって生じる化学結合であり、結合は非常に強い。分子は共有結合により形成され、
共有結合によって形成される結晶を共有結合結晶と言う。」
それに対して金属接合については説明文とポンチ絵を見ただけでは、なかなか理解ができません。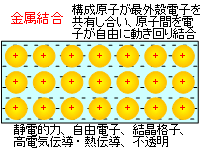「金属結合とは、金属で見られる化学結合である。金属原子はいくつかの電子を出して陽イオン（金属結晶の格子点に存在する正電荷を持つ金属の原子核）と、自由電子（結晶全体に広がる負電荷をもったもの）となる。規則正しく配列した陽イオンの間を自由電子が自由に動き回り、これらの間に働くクーロン力（静電気力、静電引力）で結び付けられている。」マイナスの電荷を持つ自由に動き回っている電子の海に、プラスの電荷の金属イオンを放り込むと、
金属イオン同士は互いに斥力により反発しあうので規則的な配列となり、金属イオンの間を自由に動き回っているマイナス電荷の電子との間に働く引力により稠密な配列に固定される。とイメージしたほうが分かりやすく感じますが、主客が転倒してしまいます。ポンチ絵に記述したように、構成原子が最外殻電子を共有し合い、その電子は格子状に配列した金属原子の間を自由に動き回る、と感じるべきなのでしょう。
金属の場合はやはり結晶格子のイメージで理解するのが簡単には思いますが、この場合には金属原子同士を格子状に結合する力は何かということが分からなくなります。
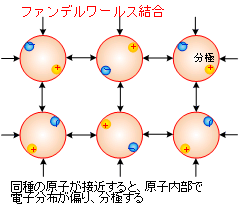
最後に、弱い結合としてファンデルワールス結合があります。説明としては、「同種の原子が接近すると、原子内で電子の分布が偏り、分極が生じるために発生する原子間の弱い結合力。」となっています。何となく分かるような、分からないような、不思議な気分です。化学系の量子論をもう少しきちんと勉強して、量子論の電子軌道を頭に叩き込んでおくべきであったと感じてしまいます。
次ページ 2016.03.12作成 2017.05.11改訂
