3.11 温度と熱の伝達
溶接では熱の伝達(移動)と温度とが重要なファクターです。熱(heat)の定義は、温度の異なる二つの物体間で起こるエネルギの移動です。熱も仕事の概念と同様に、系の境界に現れるもので、経路に依存します。言葉の意味自体はエネルギの移動ですが、方向や状態を明確にするために、熱の出入り、熱の流れ、熱の吸収・放出のように具体的な状況をはっきりさせて用いられます。熱の移動には(1)伝導(2)対流(3)放射という三つの機構があります。二つの物体間あるいは一つの物体内部に温度差が存在するとき、高温度領域から低温度領域へと熱が移動します。固体内部の熱伝達は主に伝導によります。液体内部では対流が主流で伝導はあまり寄与しません。気体の熱伝達も対流が主流ですが、プラズマ内部では輻射(放射)、対流及び伝導の全てが作用します。
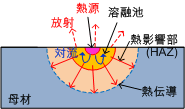
右図は溶接中の主な熱の流れを、溶接進行方向に垂直な断面について示しています。このポンチ絵では、アーク熱源から母材へと熱が注ぎ込まれて一部分が溶融します。高温度になり溶融した領域からは一部が熱放射で放出されて出て行きます。固体部分からも熱放射で外部に放出されますがその量はあまり大きくはありません。溶融金属内部では表面中心近くの高温度領域から溶融部(液体)と固体部の界面方向に、対流と熱伝導により熱が移動します。個体内部では主に熱伝導により熱が移動します。
(1)熱伝導
高温度領域の構成分子の激しい熱運動エネルギが、分子間力作用により次々に隣接する分子へと伝えられて、低温度領域にまで到達する熱の移動が熱伝導です。
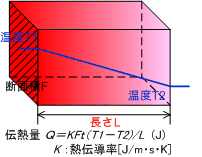
右図において、断面積F(m^2),長さL(m)の棒の左端の温度をT1、右端の温度をT2(T1>T2)とします。左端の高温部から右端の低温部へ流れる熱量Qは、単位長さあたりの温度降下(T1−T2)/Lと断面積F、時間tに比例し、上図下端の式で表現されます。
任意の等温面を通って微小時間dtの間に流れる熱量dQは次式で表されます。
dQ=−kFdt(dT/dx)
(この式は、原子の拡散に関するフィックの第一法則と似た形になっています。)
このような考え方をベースにして断面積の等しい物体の3次元の熱の流れを整理すると、下記の熱伝導率の式が導かれます。
Q=−kF(T1−T2)/L ・t
時間tに物体を伝わる熱量Qは、両端の温度差(T1−T2)と物体の断面積Aと時間tのそれぞれに比例し、長さLに反比例します。
金属の熱伝導度と電気伝導度の比は、絶対温度に金属の種類によらない定数(ローレンツ数)をかけたものに等しいというウィーデマン−フランツの法則が知られていて、その関係は次式で与えられます。
L(Lorenz constant) =k/σT
ここで、σは電気伝導率、Tは絶対温度、Lは長さではなくローレンツ数と呼ばれる定数です。もし、熱エネルギが完全に自由電子のみによって運ばれるのであれば、Lの理論値2.44×10^-8Ω・W/K^2は、温度には依存せず、すべての金属に対して同じ値になることになります。実際、この理論値は実験値に対して高々2倍程度とかなり精度良く一致しています。プラズマ分野で通常使われるローレンツ数は、プラズマ流体の速度の光速度に対する比(Nlo)なので、同じ名前の数が出現すると少し困惑します。
不純物を含ませて合金化された金属では、不純物原子が、特に固溶体においては、散乱中心として作用し電子の運動を妨げます。この結果、電気伝導率はかなり小さくなり、熱伝導率も低下します。ステンレスは合金成分を多く含むため、電気を通しにくく、熱もかなり通しにくくなります。
空気やシールドガスの密度は母材に比べて小さいため、構成分子の衝突頻度は小さく、熱伝導率は小さい値となります。衣服は布地の中に空気を捉えているため、その空気が断熱材として作用します。
以上伝導に関して簡単にまとめましたが、伝導自体はマクロな概念だけで理解しても差し支えないと感じています。以下に示す、対流と放射はマクロな概念だけでなく、分子運動論的(統計学的)にも考える必要があります。
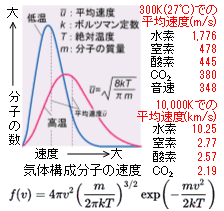
空間を二つに仕切る断熱性の幕があり、右側には右図の赤色の速度分布を持つ熱い気体があり、左側には青色の速度分布を持つ冷たい気体があると考えます。その状態では、右側は熱いまま、左は冷たいままの状態を保ちます。もし、その幕に分子が通り抜けることのできる孔が開いていれば、右の熱い気体の一部はその速度分布に比例した量が右から左に移動します。同時に、左の冷たい気体からは青色の速度分布に比例した量が左から右に移動します。結果的に、右の熱い気体は流入してくる冷たい気体分子により冷却され、逆に左の気体は加熱されます。これが、分子運動論的な熱伝導です。
マクスウエルはこの小さい穴に番人(デーモン)がいて、右側の気体から来る粒子の内、上の図の赤と青が等しくなった速度より低い速度の粒子がきたときには門を開け、高い粒子がきたときに門を閉じ、また、逆に左側の冷たい気体からくる粒子の内、両者の等しい速度より高い成分の時には門を開け、低い成分のときに門を閉じることを考えました。この場合、右の熱い気体の温度は上がり、左の冷たい気体の温度は下がることになります。この状況は実際にはありえませんが、確率的に絶対ないとはいえず、マクスウエルの悪魔として知られています。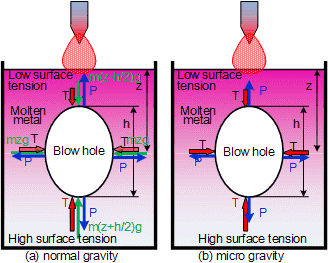
(2)対流
液体と気体では、熱伝導により一部の熱は伝わりますが、構成分子の空間的な移動はほとんど束縛されていないため、ほとんどの熱は流体自身の運動により伝達されます。高温度領域と低温度領域の密度の差や表面張力の差などにより生じる流体の運動を対流と言います。アークプラズマでは電磁気力による流れも無視できません。
右上の図は、地上と微小重力環境での溶融金属中の気泡に作用する力の関係を示しています。気泡の内部は、気泡上部の液面圧力とその位置における表面張力の和にほぼ等しい圧力が作用しています。気泡の内部での圧力差はほとんどありませんが、ブローホールに作用する液体からの力は、液体密度の水頭圧分高くなっています。底部に作用する外力が最大となり、気泡を押し上げる駆動力となります。同時に、溶融金属内部の温度も場所により異なり、表面近くは温度が高く、底部は温度が低くなります。一般的には温度が高い場合が表面張力は小さく、気泡に接触している液面は、表面張力の弱い上部から下部へと引き下げられます。この力も気泡を上方に引き上げる駆動力となります。実際、微小重力下のアーク溶接実験で気泡が外部に放出する状況を観察しています。
浮力による対流を説明しやすくするために、密度が極めて異なる気泡と溶融金属とを用いました。対流は、浮力を生じる原因により、熱対流と組成対流とに分けられます。上の説明では、溶融金属と気泡(ガス)とで成分と状態による密度の差で発生する対流を組成対流と呼び、温度によって物質の密度が変化して生じるものを熱対流と呼びます。
日常的に対流現象を観察できるのは、さめにくい材質のお椀に注がれた味噌汁の内部です。味噌汁は茶碗の側面と底面に接しており断熱状態となっています。一方、表面は冷たい外気に接して冷やされています。このため、表面近傍にある汁密度は高くなり、底面近傍の暖かい汁より重くなり沈降を始めます。入れ替わりに底面近傍のあたたかくて軽い汁は上昇します。上昇して表面近くに来た軽い汁は外気に冷却されて重たくなり沈降していきます。
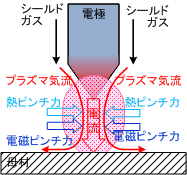
右図に示すアークプラズマ中でもプラズマ(ジェット)気流という対流が生じています。開かれた空間での流れであるため循環流にはなっていませんが、アーク中心軸に緊縮されたプラズマ成分の圧力が高くなり、圧力の低い母材側へと100m/s程度の高速度で流れています。
溶融金属(溶融池)表面に照射される熱源温度(密度)分布形状により。高温度領域の温度分布が決まり、溶接材の形状や素材特性により凝固領域形状がある程度決まります。実際には、溶融金属内部での溶融金属の対流により溶融金属内部の温度分布が変化し、その温度分布と凝固部の温度分布との相互作用とにより、溶接金属の形状と熱影響部(HAZ)の特性が決まります。
(3)放射
高温の物体から光や外線などの電磁波が放射され、空間を伝わって低温の物体に衝突・吸収されてエネルギが移動する現象が熱放射です。電磁波は真空中を光速度で伝わり、熱放射エネルギも光速度で伝わります。詳細は、「3.7 放射光」で紹介しています。
以上熱の伝達について簡単に紹介しました。対流や放射については地球内部や海洋あるいは季節風など、最近は結構頻繁に解説されていることから、なじみは深いと思います。アーク溶接の場合には、非常に狭い領域で極端な温度差が生じていることに特徴があります。また、界面での熱の授受は通常は弾性衝突で考えられますが、プラズマの熱授受は非弾性衝突によります。溶接の場合には、非常に狭い領域でなおかつ複雑な多成分要素の、電離・再結合や吸着あるいは溶融・凝固・蒸発・昇華などの物理反応と酸化や還元の化学反応が同時に生起しており、過渡的で非可逆な複雑系現象という特徴を有しています。通常の数値解析では、主要な限定的な組成の系を比較的単純な原理に基づいて計算しています。最近では計測器の精度と機能が向上したため、複雑な系についても計測が行えるようになり、同時にシミュレーションも複雑な系を対象にする様になってきています。
次ページ 2016.4.13作成 2026.01.11改訂